This was part of a recursion assignment in Computer Science I taught by Dr. Cazalas at UCF.
Assignment Specification
You are working on an engineering project with other students and are in need of 2x4s (2 by 4’s) of various lengths. Thankfully, UCF has its very own “Depot” store: KnightsDepot…so you don’t have to drive far. Unfortunately, KnightsDepot only carries 2x4s in fixed lengths. So your team will have to purchase the 2x4s and then cut them as needed. Because of your tight college student budget, you want to buy the least number of 2x4s in order to cover the lengths requested by your team.
The recursive function you are designing will return the minimum number of 2x4s you need to purchase, in order to cover the lengths requested by your team. Example:
Array of 2x4 lengths requested by your team: { 6, 4, 3, 4, 1, 3 } Fixed length of 2x4s at KnightsDepot: 6 (so each purchased 2x4 has a length of 6) A possible arrangement of of 2x4s: { 6 } { 3, 3 } { 4, 1 } { 4 } Minimum number of 2x4s needed to purchase: 4
Approach to solving
-------------------
My initial thought to solve this was to use a "greedy" algorithm which simply makes the best possible choice for the next board so that no scrap is wasted.
This method of solving is certainly faster than the final solution, but it is possible for this method not to be the most efficient use of boards.
The correct solution was to permutate the order in which you bought the boards and do a simple in-order purchase and calculate if this order performed better than the previous.
``` c KnightsDepot.c
/* precondition: fin/fout are pointers to the input/output file
postcondition: calculates the minimum amount of boards needed for project
*/
void KnightsDepot(FILE *fin, FILE *fout) {
//read in args
int size, whole;
fscanf(fin, "%d %d", &whole, &size);
if (DEBUG) printf("Read in argument size: %d, whole: %d\n", size, whole);
//need to DAM for board array
int * boards = (int *) malloc(sizeof(int)*size);
//read in boards
int i;
for (i=0; i < size; i++)
fscanf(fin, "%d", &boards[i]);
//begin solving
if (DEBUG) printf("KnightsDepot: \n");
fprintf(fout, "KnightsDepot: ");
//edgecase: if boards to be bought are zero then just print 0 and get out
if (size == 0) {
fprintf(fout, "%d\n\n", 0);
if (DEBUG) printf("\ntotal boards: %d\n\n", 0);
return;
}
//for passing by reference into DepotPermuteAndCalc
//setting value to -1 indicates no boards have been counted yet.
int runningCount = -1;
//recurse
int total = DepotPermuteAndCalc(boards, size, 0, whole, &runningCount);
fprintf(fout, "%d\n\n", total);
if (DEBUG) printf("\ntotal boards: %d\n\n", total);
//cleanup
free(boards);
return;
}
/* precondition: boards is the array of our board lengths of size size. fixed is the range we are holding
in place [0-fixed] while we permute. whole is the dimension of the boards at the store and
runningCount is a pointer which holds the value of the least amount of boards we purchased
through all the permutations.
postcondition: returns the minimum number of boards needed for the project.
*/
int DepotPermuteAndCalc(int boards[], int size, int fixed, int whole, int *runningCount) {
if (DEBUG) {
printf("PermutateAndCalc() size:%d, fixed:%d, whole:%d, runningCount:%d\n", size, fixed, whole, *runningCount);
int i;
for (i=0; i<size; i++)
printf("%d ", boards[i]);
printf("\n");
}
//basecase
if (fixed == size) {
//calculate number of boards needed for this permutation
int count = DepotCalcBoards(boards, size-1, whole);
//compare to past permuations or just set it to runningCount if this is first permutation (-1)
if (*runningCount == -1 || count < *runningCount)
*runningCount = count;
}
//permutate
int i;
for (i=fixed; i < size; i++) {
swap(boards, fixed, i);
DepotPermuteAndCalc(boards, size, fixed+1, whole, runningCount);
swap(boards, fixed, i);
}
//return our lowest count
return *runningCount;
}
/* precondition: boards is the array of our board lengths of size size. whole is the dimension of the boards
at the store.
postcondition: returns the number of boards needed doing a 'dumb' linear addition
*/
int DepotCalcBoards(int boards[], int size, int whole) {
int i;
int working = 0;
//start at the end of the array and figure out how many boards we can get
for(i=size; i >= 0; i--) {
working += boards[i];
//the boards divide evenly into the whole dimension
if (working == whole) {
//are we at the end of array?
if (i == 0) return 1;
//no so recurse
else return 1 + DepotCalcBoards(boards, i-1, whole);
}
//we have to waste the rest of the board and recurse with current i as new size
if (working > whole) return 1 + DepotCalcBoards(boards, i, whole);
}
//if we get this far then we have a stray cut that needs to be made
return 1;
}
/* precondition: a is the position that will be put into b and vice-versa
postcondition: switches the values at index a and index b in the array
*/
void swap(int array[], int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
return;
}
```


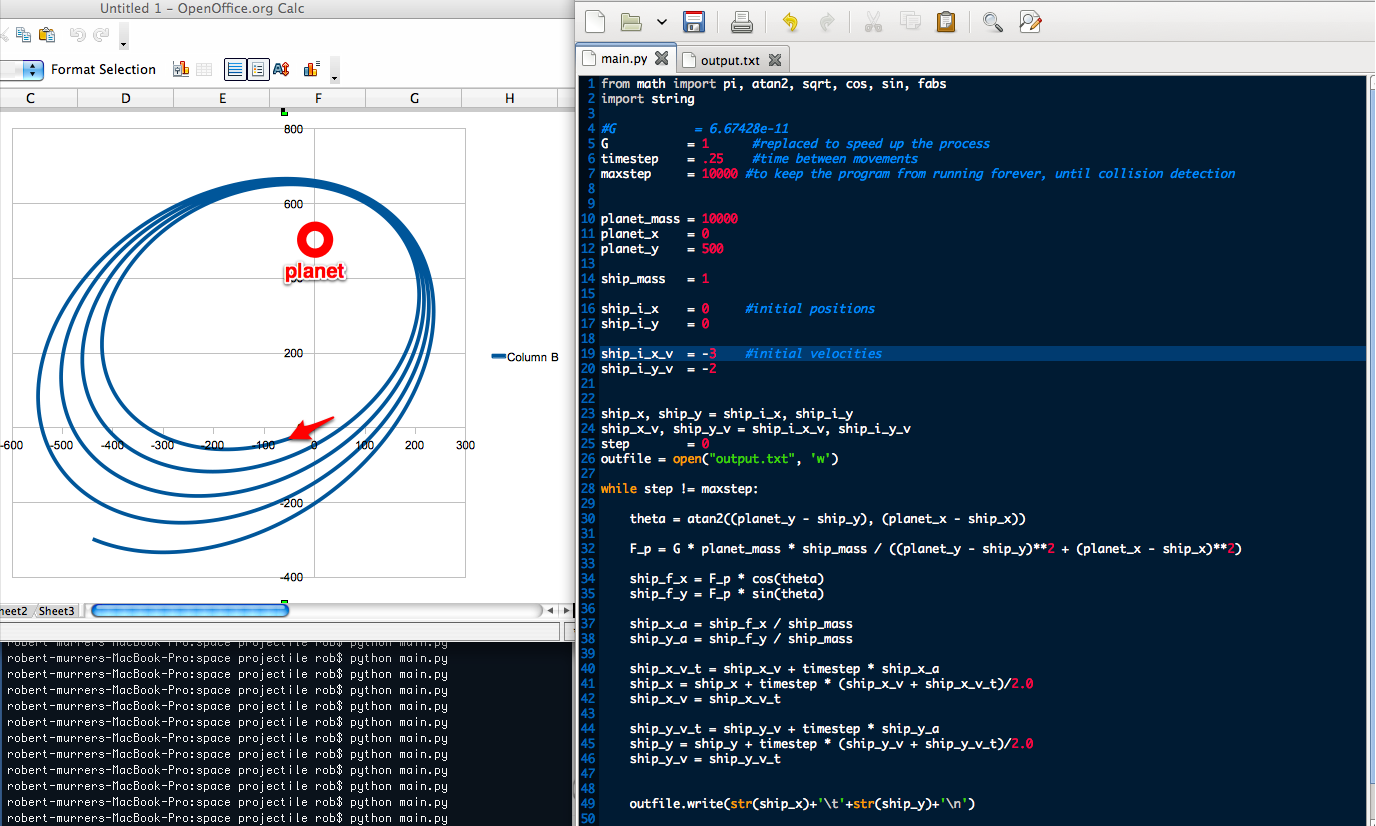











 This is the overlay of a 960 grid and a 21px typsetting guide.
This is the overlay of a 960 grid and a 21px typsetting guide.